Collaborative Filtering for Implicit Feedback Datasets

implicit한 feedback을 추가해서 추천시스템을 만들 수 있다.

* purchase history, browsing history, search patterns, mouse movements..

implicit feedbak의 특징

1. negative 한 feedback이 없다.

implicit feedback을 보고 user가 좋아하는지, 좋아하지 않는지 알 수 없다. 유저가 어떤 영화를 봤지만 싫어할 수 있기 때문이다. missing data의 경우 부정적인 피드백일 가능성이 높기 때문에 missing data에 대해서 어떻게 처리를 할지 고려해야 한다.(missing data= no action)

2. 근본적으로 nosiy가 많다.

예를 들어, 한 아이템을 구매했지만 선물용으로 구매했을 수 있고, 그 물건에 대해 실망할 수 있기 때문이다. 또, TV 프로그램을 시청했지만 잠들었을 가능성도 있다.

3. explicit feedback은 preference를 나타내지만, implicit feedback은 confidence를 나타낸다.

위에서 설명한것과 같이 implicit feedback이 user의 선호도와 다를 수 있다. 하지만, 1번 implicit feedback을 나타낸 것과 여러번 implicit feedback을 나타낸것은 확연히 다르며 신뢰도가 높은 데이터라고 생각할 수 있다.

4. implicit feedback의 평가방법

explicit의 경우 RMSE등을 사용할 수 있다. 그 이유는, 고객이 평점을 매겼기 때문에 numeric score를 정의할 수 있기 때문이다.

implicit의 경우 item availability, 아이템들의 competition, repeat feedback을 고려해야 한다.

item avilability는 동시간에 방영되는 두 TV Show의 경우 한쪽만 볼 수 있어서 다른 프로그램을 좋아한다고 해도 Implicit Data가 쌓이지 않는 상황을 말한다. repeat feedback의 경우는 3번과 마찬가지로 한번 feedback을 준것과 여러번 준것은 신뢰도가 다르기 때문에 고려해야 한다.

model

$p_{ui}$는 선호도로 user가 item을 소비했다면 1, 아니라면 0이라고 정의한다. 1이라는 뜻은 user가 item을 선호한다는 뜻이다. 하지만, binary하게 점수를 매겨버린다면 소비를 했냐 안했냐에 따라 선호도가 정해지기 때문에 보완이 필요하다. 이를 신뢰도(confidence)로 보완하겠다. 즉, item 1을 한번 산 사람과, 100번 산 사람의 신뢰도를 다르게 보는 것이다. rating이 커질수록 user가 item을 좋아한다고 판별하기 때문에 신뢰도가 높아지도록 설계했다.

$c_{ui}= 1+\alpha r_{ui}$

여기서 $\alpha$로 증가율을 컨트롤한다.

* 여기서 제안하는 confidence 계산의 또다른 방법

$$c_{ui}= 1+\alpha log(1+r_{ui}/\epsilon)$$

따라서 기존에 있던 loss function을 다음과 같이 변형시킬 수 있다.

기존의 loss funtion에서 rating 대신 confidence, Preference를 이용해 implicit한 데이터를 적용할 수 있다.

optimizer

위의 loss function을 미분하면 optimizer가 나온다. 공식 유도는 여기를 참고하면 된다.

공식유도를 볼 때 전치행렬의 미분이 이해가 되지않았다. 행렬의 미분은 여기를 참고했다.

즉, 전치행렬을 미분해보면 각각 $x_i$가 자기자신을 미분하기 때문에 1이되고, 위의 $x^T_uy_i$에서 $x^T_u$=1이 성립해 $y_i$만 남는것이다.

<공식유도>

위의 링크 참조

모든 user들에 대한 선호도는 $x_{u}= (Y^TC_uY+\lambda I)^{-1}Y^TC^up(u)$로 나타낼 수 있고, item에 대해서 표현하고 싶다면, u와 i를 서로 바꿔주면 된다.
이를 통해 preference를 similarity와 confidence로 표현할 수 있는데, 이를 유도해보자.
$\hat{p_{ui}}= y_i^Tx_u$이다. 여기서 $x_{u}= (Y^TC_uY+\lambda I)^{-1}Y^TC^up(u)$ 이기 때문에 $\hat{p_{ui}}= y_i^T(Y^TC_uY+\lambda I)^{-1}Y^TC^up(u)$로 표현할 수 있다.
$(Y^TC_uY+\lambda I)^{-1}$ 를 가중치 매트릭스 $W^u$라고 둔다면, similarity 는 $s^u_{ij}= y_i^TW^uy_j$가 된다.
$\hat{p_{ui}}= \Sigma s_{ij}^uc_{uj}$

위의 공식처럼 전개해버리면, $Y^TY$는 user에 대한 iterate가 필요없기 때문에 불필요한 반복을 줄여 시간적인 개선을 할 수 있다.

이것은 우리의 latent model을 과거 행동의 선형 함수로 선호도를 예측하는 선형모델로 축소시킵니다. 모든 과거의 행동들은 예측된 pui로 나타내지고, 우리는 이것들의 관여를 독립시킬수 있습니다. 가장 높은 기여를 한 행동은 추천의 가장 적합한 설명이 될 것입니다. 게다가 우리는 모든 개인들의 과거 행동을 u와 신뢰도 간의 관계, 아이템 i와 su의 유사성으로 분리시킬 수 있습니다. 이 모델은 neighborhood 모델의 강력한 전처리 용 모델로 사용할 수 있는데, 아이템 유사도가 최적화의 과정을 통해 학습되기 때문입니다. 게다가 아이템 사이의 유사도는 특정 사용자에 의존됩니다.

import pandas as pd
import numpy as np
import time
import scipy.sparse as sparse
from scipy.sparse.linalg import spsolve

train_df = pd.read_csv( ("train.csv"))
# ("../../MovieLens 100K/data/ratings.csv")

R = train_df.values
P= np.copy(train_df)
P[P>0]=1
alpha = 40
C = 1 + alpha * R

r_lambda= 40
nf= 200
nu= train_df.shape[0]
ni= train_df.shape[1]

# latent
X= np.random.normal(size=(train_df.shape[0], nf))
Y = np.random.normal(size=(train_df.shape[1], nf))

def loss_function(C, P, xTy, X, Y, r_lambda):
    predict_error = np.square(P - xTy)
    confidence_error = np.sum(C * predict_error)
    regularization = r_lambda * (np.sum(np.square(X)) + np.sum(np.square(Y)))
    total_loss = confidence_error + regularization
    return np.sum(predict_error), confidence_error, regularization, total_loss
    
 
def optimizer_user(X, Y, C, P, nu, nf, r_lambda):
    yT = np.transpose(Y)
    for u in range(nu):
        Cu = np.diag(C[u])
        yT_Cu_y = np.matmul(np.matmul(yT, Cu), Y)
        lI = np.dot(r_lambda, np.identity(nf))
        yT_Cu_pu = np.matmul(np.matmul(yT, Cu), P[u])
        X[u] = np.linalg.solve(yT_Cu_y + lI, yT_Cu_pu)
        
def optimizer_item(X, Y, C, P, ni, nf, r_lambda):
    xT = np.transpose(X)
    for i in range(ni):
        Ci = np.diag(C[:, i])
        xT_Ci_x = np.matmul(np.matmul(xT, Ci), X)
        lI = np.dot(r_lambda, np.identity(nf))
        xT_Ci_pi = np.matmul(np.matmul(xT, Ci), P[:, i])
        Y[i] = np.linalg.solve(xT_Ci_x + lI, xT_Ci_pi)
        
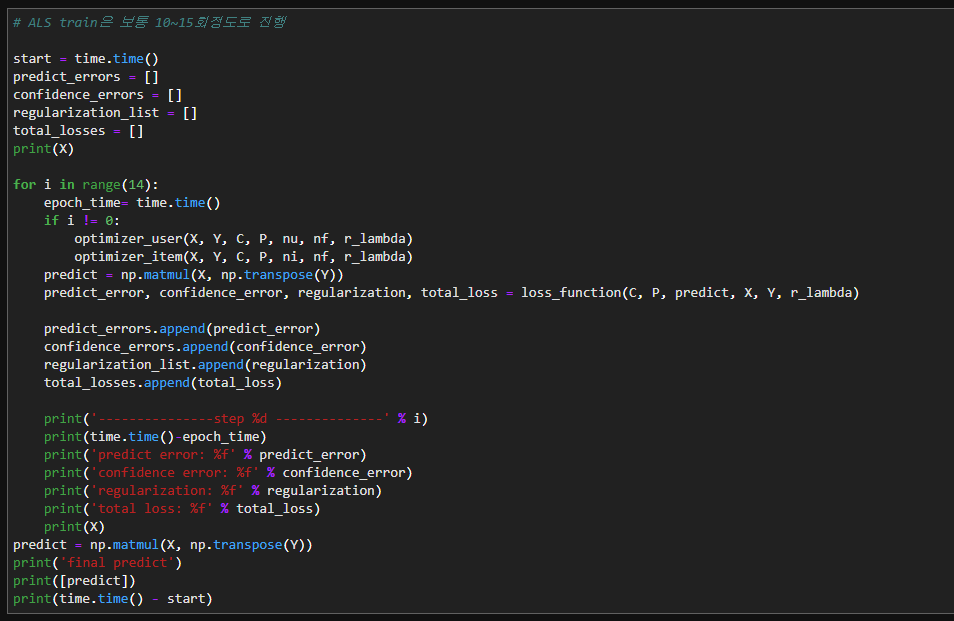
# ALS train은 보통 10~15회정도로 진행

start = time.time()
predict_errors = []
confidence_errors = []
regularization_list = []
total_losses = []
print(X)

for i in range(14):
    epoch_time= time.time()
    if i != 0:
        optimizer_user(X, Y, C, P, nu, nf, r_lambda)
        optimizer_item(X, Y, C, P, ni, nf, r_lambda)
    predict = np.matmul(X, np.transpose(Y))
    predict_error, confidence_error, regularization, total_loss = loss_function(C, P, predict, X, Y, r_lambda)
    
    predict_errors.append(predict_error)
    confidence_errors.append(confidence_error)
    regularization_list.append(regularization)
    total_losses.append(total_loss)
    
    print('---------------step %d --------------' % i)
    print(time.time()-epoch_time)
    print('predict error: %f' % predict_error)
    print('confidence error: %f' % confidence_error)
    print('regularization: %f' % regularization)
    print('total loss: %f' % total_loss)
    print(X)
predict = np.matmul(X, np.transpose(Y))
print('final predict')
print([predict])
print(time.time() - start)

출처: https://yeomko.tistory.com/8

https://orill.tistory.com/entry/Explicit-vs-Implicit-Feedback-Datasets [이제 며칠 후엔]

https://jessesw.com/Rec-System/