
import & data
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('seaborn')
sns.set(font_scale=2.5) # 이 두줄은 본 필자가 항상 쓰는 방법입니다. matplotlib 의 기본 scheme 말고 seaborn scheme 을 세팅하고, 일일이 graph 의 font size 를 지정할 필요 없이 seaborn 의 font_scale 을 사용하면 편합니다.
import missingno as msno
import warnings
warnings.filterwarnings('ignore')
%matplotlib inlin
df_train.head()
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
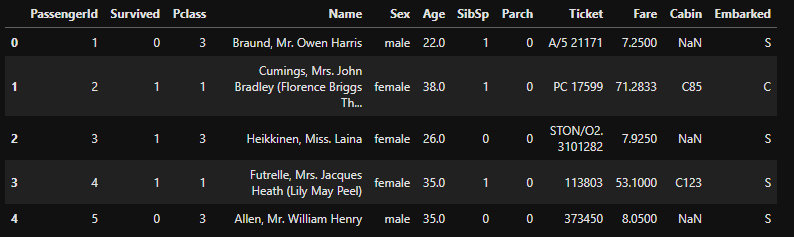
1. Null Data Check
- 아래의 코드를 실행하면 각 column별로 null값의 비율을 확인할 수 있다.
train data, test data를 따로 확인함.
|
1
2
3
4
5
6
7
|
for col in df_train.columns:
msg = 'column: {:>10}\t Percent of NaN value: {:.2f}%'.format(col, 100 * (df_train[col].isnull().sum() / df_train[col].shape[0]))
print(msg)
for col in df_test.columns:
msg = 'column: {:>10}\t Percent of NaN value: {:.2f}%'.format(col, 100 * (df_test[col].isnull().sum() / df_test[col].shape[0]))
print(msg)
|
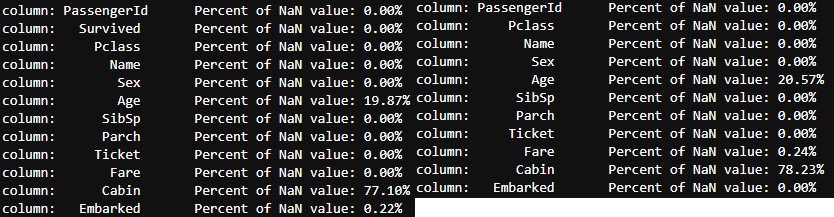
- 그래프로 한눈에 null 분포를 확인할 수 있다.
|
1
|
msno.matrix(df=df_train.iloc[:, :], figsize=(8, 8), color=(0.8, 0.5, 0.2))
|
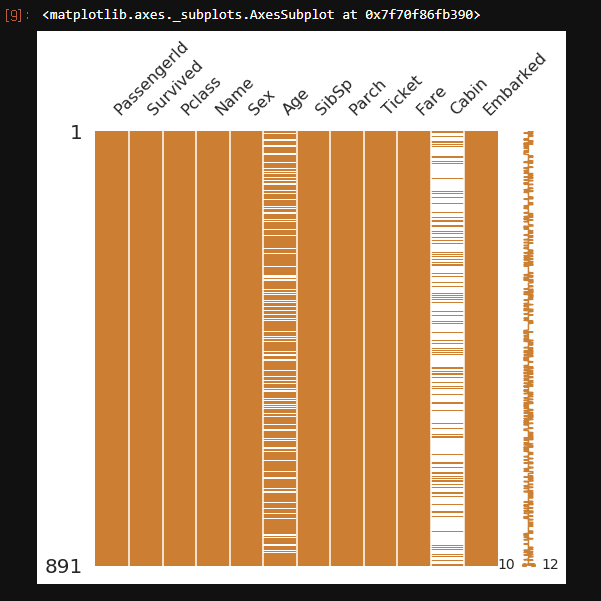
1.2 Target label 확인
모델을 설계하기 전 target label의 분포를 확인해야 한다. 특히, binary classification의 경우에서, 1과 0의 분포가 어떠냐에 따라 모델의 평가 방법이 달라진다.
이때까지 데이터분석을 하면서 Target label의 분포를 확인해본적이 없는데, 데이터 분석을 들어가기전에 꼭 거쳐야 할 과정인것 같다.
만약, 0과 1이라는 label이 있는데 한 값에 너무 편중되어 있다면 데이터셋의 크기를 어느정도 맞춰주는 sampling방식을 사용해야한다.
만약, 0이 10개 1이 90개가 있다고 생각하자. sampling의 방식으로 3가지가 있는데 0의 데이터를 늘려 90개와 비슷하게 만들어 주는 방법, 1의 데이터를 줄여 10개와 비슷하게 만들어 주는 방법, 1은 데이터를 줄이고 0은 늘려 두 데이터의 분포를 비슷하게 만들어주는 방법이있다.
이렇게, 데이터의 불균형을 맞춰주기 위해서 SMORE 패키지를 사용할 수 있다.
사실 sampling말고 weight balancing이라는 방법도 있는데, 데이터 불균형 문제에 대해서는 추후에 다루겠다.
|
1
2
3
4
5
6
7
8
9
|
f, ax = plt.subplots(1, 2, figsize=(18, 8))
df_train['Survived'].value_counts().plot.pie(explode=[0, 0.1], autopct='%1.1f%%', ax=ax[0], shadow=True)
ax[0].set_title('Pie plot - Survived')
ax[0].set_ylabel('')
sns.countplot('Survived', data=df_train, ax=ax[1])
ax[1].set_title('Count plot - Survived')
plt.show()
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
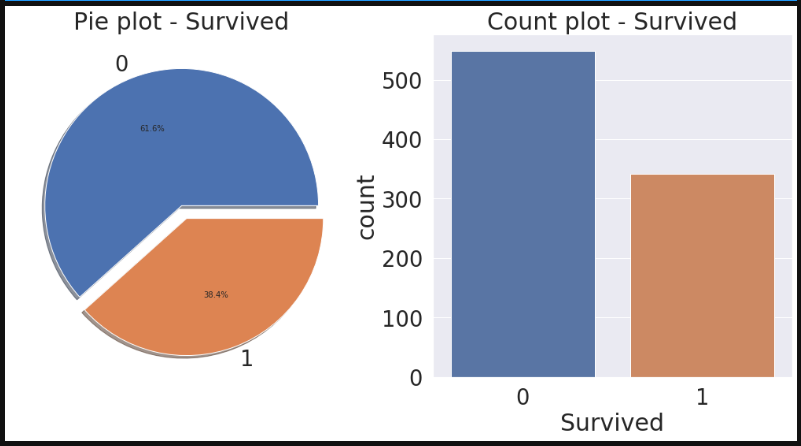
위를 보면, target label이 극단적이지 않고 균등하다.
만약, 100개 중에서 1이 99개인 극단적인 분포라면 모두 1로 예측해도 정확도가 높기 때문에 평가방법이 달라져야 한다. 이 데이터는 그런 문제가 없기 때문에 넘어가겠다.
Exploratory data analysis
2.1 PClass
feature중 PClass는 서수형 데이터이다. 서수형 데이터는 카테고리와 비슷하지만, 카테고리면서 순서가 있는 데이터 타입이다.
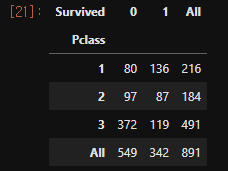
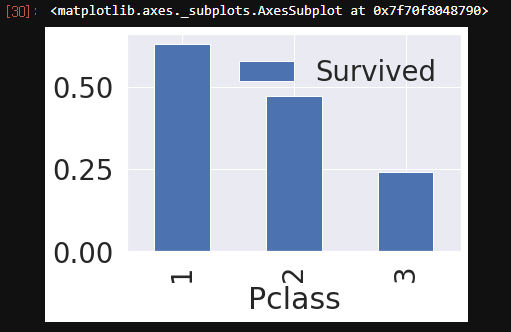
아래의 결과를 보면 class가 높을수록 생존확률이 높다.
|
1
2
3
|
# crosstab을 이용하면 count와 sum을 한번에 확인할 수 있다.
t= pd.crosstab(df_train['Pclass'], df_train['Survived'], margins=True)
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
|
1
|
df_train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True).mean().sort_values(by='Survived', ascending=False).plot.bar()
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
|
1
2
3
4
5
6
7
8
|
y_position = 1.02
f, ax = plt.subplots(1, 2, figsize=(18, 8))
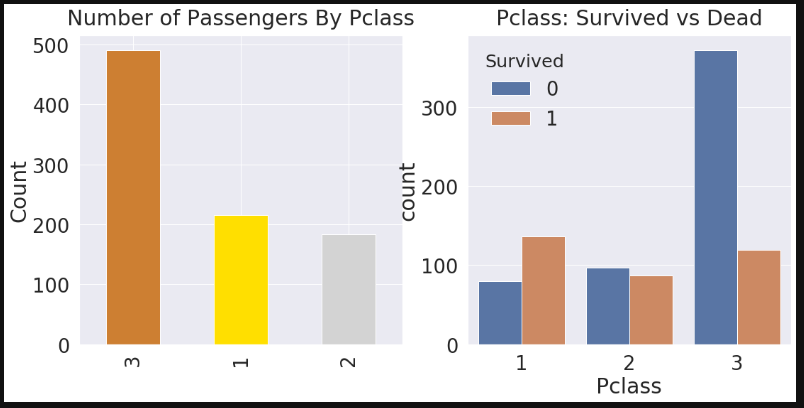
df_train['Pclass'].value_counts().plot.bar(color=['#CD7F32','#FFDF00','#D3D3D3'], ax=ax[0])
ax[0].set_title('Number of Passengers By Pclass', y=y_position)
ax[0].set_ylabel('Count')
sns.countplot('Pclass', hue='Survived', data=df_train, ax=ax[1])
ax[1].set_title('Pclass: Survived vs Dead', y=y_position)
plt.show()
|
2.2 Sex
|
1
2
3
4
5
6
|
f, ax = plt.subplots(1, 2, figsize=(18, 8))
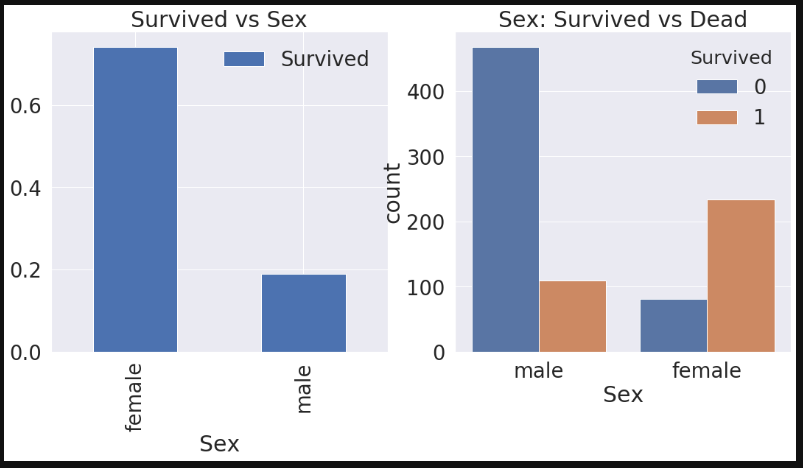
df_train[['Sex', 'Survived']].groupby(['Sex'], as_index=True).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
sns.countplot('Sex', hue='Survived', data=df_train, ax=ax[1])
ax[1].set_title('Sex: Survived vs Dead')
plt.show()
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
|
1
|
pd.crosstab(df_train['Sex'], df_train['Survived'], margins=True).style.background_gradient(cmap='summer_r')
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
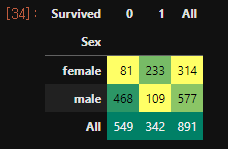
Female이 생존할 확률이 높다.
2.3 Both Sex and Pclass
sex, pclass에 관해 생종률이 어떻게 달라지는지 확인하고자 한다.
seaborn의 factorplot을 이용하면 3차원으로 이뤄진 그래프를 그릴 수 있다.
그래프를 보면, 모든 클래그에서 여자가 생존할 확률이 높으며, 클래스가 높아질수록 생존할 확률이 높다.
|
1
2
|
sns.factorplot('Pclass', 'Survived', hue='Sex', data=df_train, size=6, aspect=1.5)
|

2.4 age
- 나이별 생존율
|
1
2
3
4
5
6
7
8
9
|
print('제일 나이 많은 탑승객 : {:.1f} Years'.format(df_train['Age'].max()))
print('제일 어린 탑승객 : {:.1f} Years'.format(df_train['Age'].min()))
print('탑승객 평균 나이 : {:.1f} Years'.format(df_train['Age'].mean()))
fig, ax = plt.subplots(1, 1, figsize=(9, 5))
sns.kdeplot(df_train[df_train['Survived'] == 1]['Age'], ax=ax)
sns.kdeplot(df_train[df_train['Survived'] == 0]['Age'], ax=ax)
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colors |
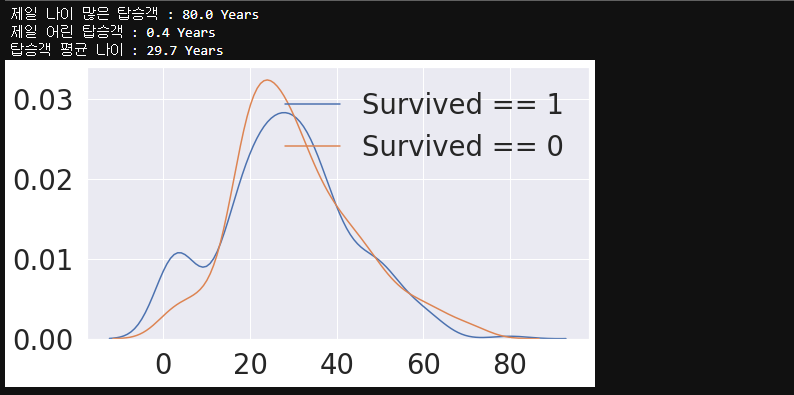
- 나이/클래스별 생존율
|
1
2
3
4
5
6
7
8
9
|
# Age distribution withing classes
df_train['Age'][df_train['Pclass'] == 1].plot(kind='kde')
df_train['Age'][df_train['Pclass'] == 2].plot(kind='kde')
df_train['Age'][df_train['Pclass'] == 3].plot(kind='kde')
plt.xlabel('Age')
plt.title('Age Distribution within classes')
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
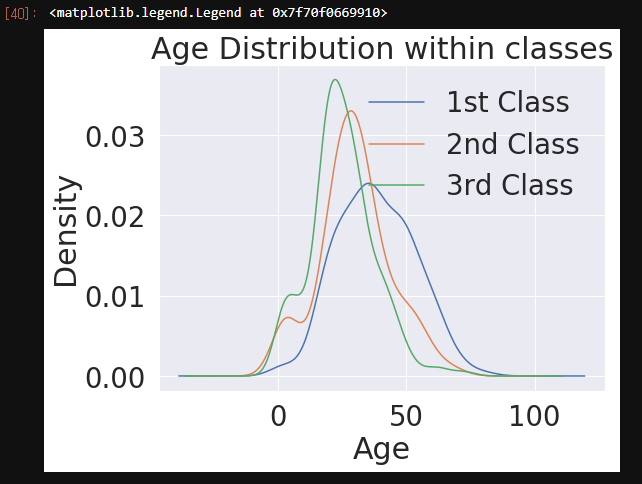
- 나이별 생존 누적분포
|
1
2
3
4
5
6
7
8
9
10
11
|
# 나이별 누적분포
cummulate_survival_ratio = []
for i in range(1, 80):
cummulate_survival_ratio.append(df_train[df_train['Age'] < i]['Survived'].sum() / len(df_train[df_train['Age'] < i]['Survived']))
plt.ylabel('Survival rate')
plt.xlabel('Range of Age(0~x)')
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
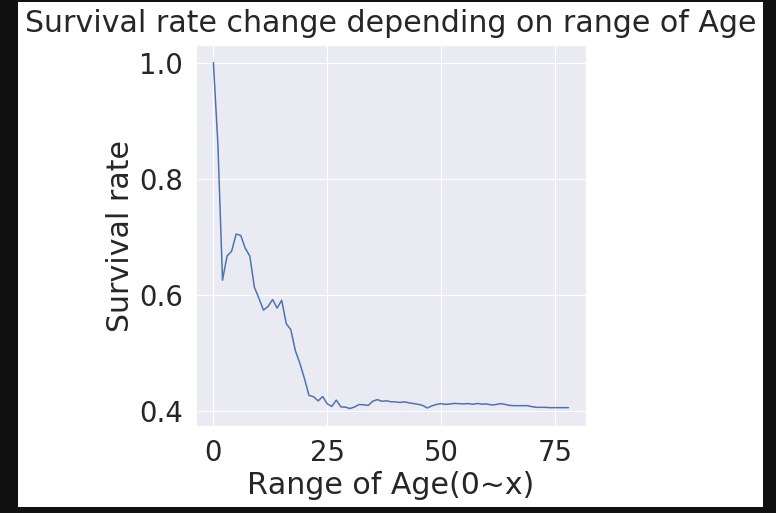
2.5 PClass, Sex, Age
3가지 요소를 종합적으로 고려해 생존율을 파악해보자. seaborn의 violinplot를 사용하면 쉽게 파악할 수 있다.
x축은 case(pcalss, sex)이며, y축은 보고싶어하는 age분포이다.
|
1
2
3
4
5
6
7
8
|
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=df_train, scale='count', split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=df_train, scale='count', split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
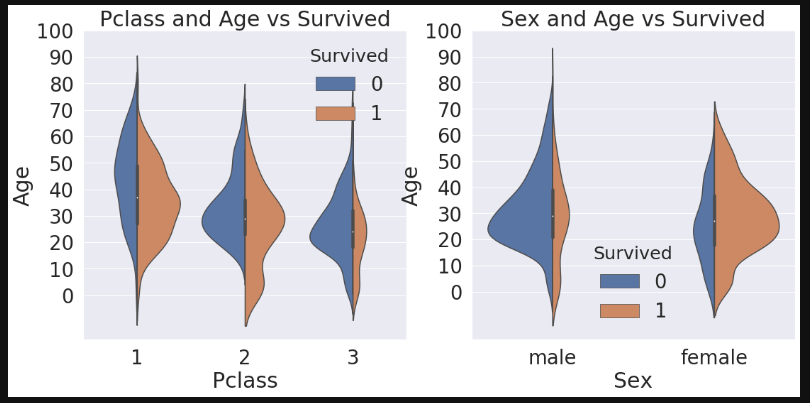
모든 클래스에서 나이가 어릴수록 생존할 확률이 높다. 또한, 명확하게 여자가 많이 생존한다.
2.6 Embarked
|
1
2
|
f, ax = plt.subplots(1, 1, figsize=(7, 7))
df_train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=True).mean().sort_values(by='Survived', ascending=False).plot.bar(ax=ax)
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
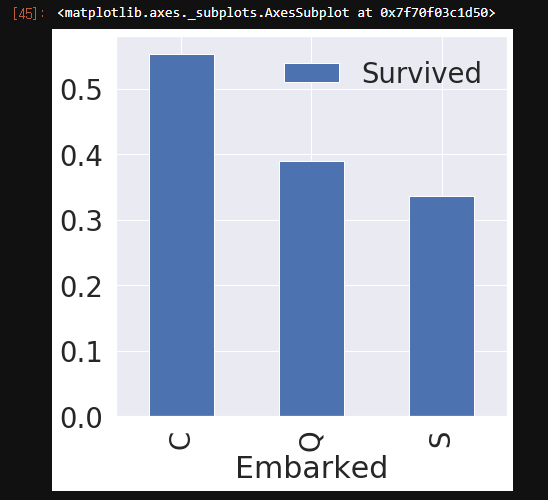
|
1
2
3
4
5
6
7
8
9
10
11
|
f,ax=plt.subplots(2, 2, figsize=(20,15))
sns.countplot('Embarked', data=df_train, ax=ax[0,0])
ax[0,0].set_title('(1) No. Of Passengers Boarded')
sns.countplot('Embarked', hue='Sex', data=df_train, ax=ax[0,1])
ax[0,1].set_title('(2) Male-Female Split for Embarked')
sns.countplot('Embarked', hue='Survived', data=df_train, ax=ax[1,0])
ax[1,0].set_title('(3) Embarked vs Survived')
sns.countplot('Embarked', hue='Pclass', data=df_train, ax=ax[1,1])
ax[1,1].set_title('(4) Embarked vs Pclass')
plt.subplots_adjust(wspace=0.2, hspace=0.5)
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
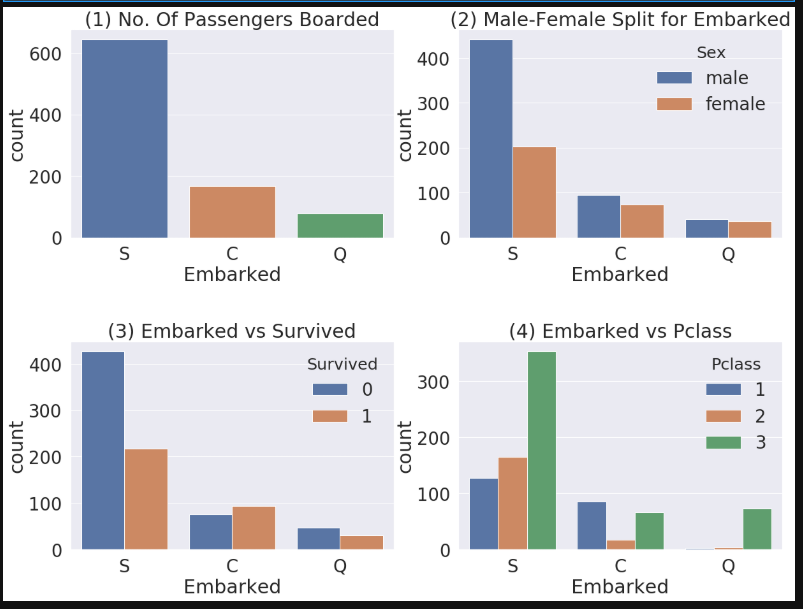
그래프를 확인해보니 확실히 S에서 탑승한 사람들이 생존율이 낮았다. 또한, 탑승항구 S는 3클래스의 탑승자가 많다.
2.7 Family-sibsp, parch
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
df_train['FamilySize'] = df_train['SibSp'] + df_train['Parch'] + 1 # 자신을 포함해야하니 1을 더합니다
df_test['FamilySize'] = df_test['SibSp'] + df_test['Parch'] + 1 # 자신을 포함해야하니 1을 더합니다
f,ax=plt.subplots(1, 3, figsize=(40,10))
sns.countplot('FamilySize', data=df_train, ax=ax[0])
ax[0].set_title('(1) No. Of Passengers Boarded', y=1.02)
sns.countplot('FamilySize', hue='Survived', data=df_train, ax=ax[1])
ax[1].set_title('(2) Survived countplot depending on FamilySize', y=1.02)
df_train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=True).mean().sort_values(by='Survived', ascending=False).plot.bar(ax=ax[2])
ax[2].set_title('(3) Survived rate depending on FamilySize', y=1.02)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
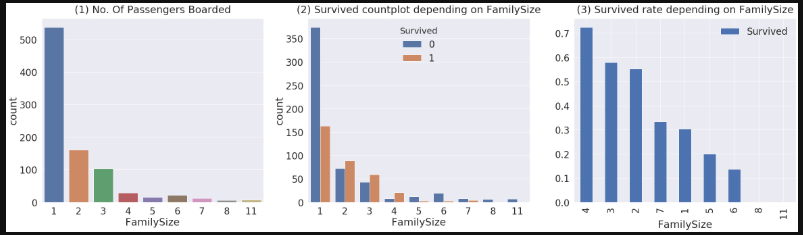
가족수가 너무 작아도, 너무 커도 생존율이 낮아지며, 3-4인 가족이 가장 생존확률이 높다.
2.8 Fare
탑승요금은 contious feature이기 때문에 histogram으로 살펴봤다.
|
1
2
3
|
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
g = sns.distplot(df_train['Fare'], color='b', label='Skewness : {:.2f}'.format(df_train['Fare'].skew()), ax=ax)
g = g.legend(loc='best')
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
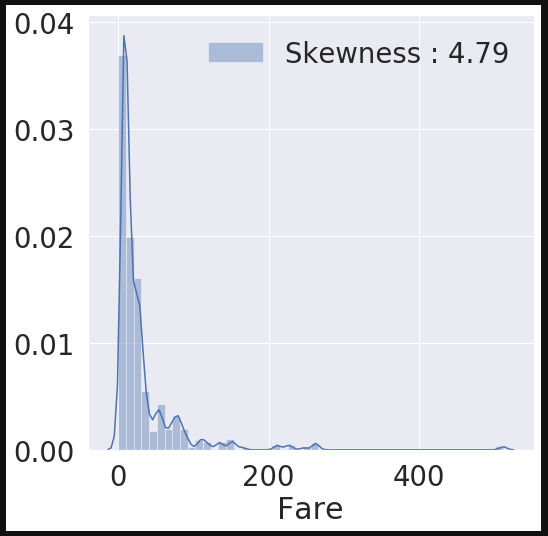
결과를 보면 분포가 매우 비대칭이다. 만약 이대로 모델에 학습한다면 잘못 학습될 수 있다. 때문에 몇개 없는 outlier의 영향을 줄이기 위해 log를 취했다.
|
1
2
3
4
5
6
7
|
df_test.loc[df_test.Fare.isnull(), 'Fare'] = df_test['Fare'].mean() # testset 에 있는 nan value 를 평균값으로 치환합니다.
df_train['Fare'] = df_train['Fare'].map(lambda i: np.log(i) if i > 0 else 0)
df_test['Fare'] = df_test['Fare'].map(lambda i: np.log(i) if i > 0 else 0)
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
g = sns.distplot(df_train['Fare'], color='b', label='Skewness : {:.2f}'.format(df_train['Fare'].skew()), ax=ax)
g = g.legend(loc='best')
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
http://colorscripter.com/info#e" target="_blank" style="text-decoration:none;color:white">cs |
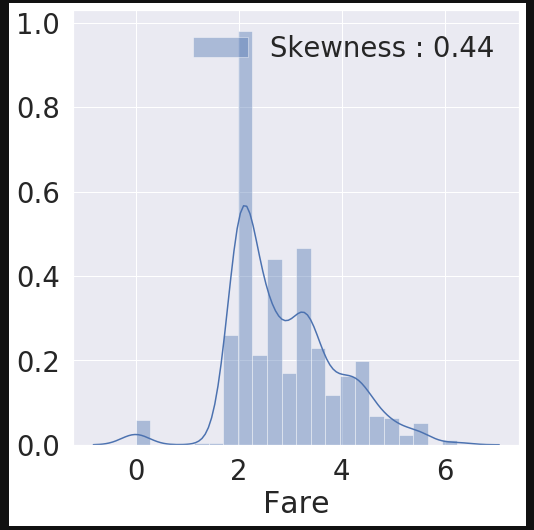
Cabin은 nan값이 너무 크기 때문에 EDA를 실시하지 않았다.
Ticket은 string data이며, 워낙 unique한 값이 많기 때문에 여러 아이디어를 적용해서 모델에 넣어야한다.
출처
'인공지능 > 캐글' 카테고리의 다른 글
| 1-3. Titanic Top 4% with ensemble (0) | 2020.04.15 |
|---|---|
| 1-2. EDA To Prediction (0) | 2020.04.15 |

