SVM을 이해하기 위해 필요한 Maximal Margin Classifier, SVC를 설명하고 최종적으로 SVM을 설명하겠다.
SVM에 사용되는 kernel, Kernel Trick도 알아보자.
아래의 내용은 https://www.youtube.com/user/joshstarmer를 보며 정리한 내용이다.
1. Maximal Margin Classifier
쥐의 무게를 보고 정상인지 비만인지 분류해보자.
임계값을 주황색 선으로 잡고, 임계값보다 작으면 주황색(정상), 크면 (비만)으로 분류하겠다.
새로운 점(초록점)이 들어온다면, 입계 값보다 크기 때문에 비만 데이터로 예측할 것이다.


하지만 만약 임계값에 가까운 검은색 데이터가 들어온다면 어떻게 될까? 임계값보다는 크기 때문에 비만으로 분류되겠지만, 정상 데이터들과 더 가깝다. 따라서 임계값을 조정해야 할 것이다.
개념
더 좋은 임계값을 찾기 위해서는 빨간색 데이터와 초록색 데이터 사이의 공간(margin)을 최대화하면 된다. 즉, 빨강 데이터와 초록 데이터의 중간지점을 임계값을 잡으면 최적의 임계값을 설정할 수 있다.
여기서는 두 클래스의 중간지점이 margin이 최대가 되는 지점이다.
* margin: 데이터와 임계값 사이의 거리
이렇게 margin이 최대가 되게 분류하는 것을 'Maximal Margin Classifier'이라고 한다.
따라서 새로운 임계값을 지정하면 이전의 검정 데이터는 초록 데이터(비만)가 아닌 빨강 데이터(정상)로 분류할 것이다.

한계
하지만 Maximal Margin Classifier은 outliner 문제가 있다. 만약 초록 데이터 범위 안에 빨강 데이터가 존재한다면 어떻게 될까? 즉, 빨강 데이터의 이상치가 존재한다면 아래와 같이 임계값을 잡게 된다. 아래의 그림에서 검정 화살표로 들어온 데이터는 초록 데이터들과 가까운 거리를 가지고 있으므로 초록 데이터로 분류하는 게 더 자연스러운 이론인데, maximal margin의 조건 때문에 새로 들어온 데이터는 빨강 데이터로 분류한다.

결국, outliner에 엄청나게 예민한 모델이 되는 것이다.
이를 misclassifications로 해결할 수 있다.
2. support vector classifier
soft margin classifier를 사용하는 것을 support vector classifier라고 한다.
miscalssifications
miscalssifications으로 outliner에 민감하지 않은 모델을 생성할 수 있다. 즉, 데이터가 outliner인지 아닌지 판별 한 뒤 임계점을 나누는 것이다. 이를 적용하면 아래와 같이 새로운 값이 들어오면, 이전의 모델과 다르게 초록 데이터로 분류한다.

soft margin
misclassifications를 적용할 때, margin을 soft margin이라고 부른다.

soft margin을 어떻게 정의할까?
soft margin은 모든 점에 대해서 cross validation으로 outlier를 판별하고, 가장 최적의 임계값을 찾아낸다. 그림을 보면 더 잘 이해될 것이다.

이렇게, 모든 점에서 반복하면 최적의 임계값이 다음과 같이 나오게 되고, 다음을 임계값으로 지정하면 misclassification은 1개이며 나머지는 모두 정상적으로 분류할 수 있다.

이때까지 모두 1차원에서만 데이터 분류를 해봤다. 그렇다면 2차, 3차원에서는 어떻게 될까?
결론적으로, 1차원은 0차원의 subspace, 2차원은 1차원 subspace(경계선), 3차원은 2차원 subspace(경계면)가 경계의 역할을 한다.
3차원 이상의 4차원부터는 경계선, 경계면이 아니라 초평면이라 한다. 또한, 경계선 경계면 등은 모두 초평면에 포함된다
soft margin은 hard margin과 거의 비슷하다. hard margin 목적식에 regularization term이 붙는다.
$\underset{w,b,\xi}{minimize} \frac{1}{2}||w||_2^2+C\sum\xi_i$
즉, 에러를 어느정도 결정한다는 것이다.
그 전과 다르게 결정하는 변수는 에러($\xi$)가 생겨 총 3개($w,b,\xi$)가 된다.
여기서 C는 hyperparameter이며 training error를 얼마나 허용할 것인지를 결정한다. 즉, C가 크면 training error를 많이 허용하지 않아 overfitting이 될 가능성이 크다.
제약식을 푸는 방법은 기존의 hard margin처럼 풀면 되는데, $\xi$값도 구해야 하기 때문에 총 3개의 미지수를 미분하면 된다.
아래의 링크에 잘 정리되어 있으니 정리하지 않겠다.(10:30참고)
https://www.youtube.com/watch?v=ltjhyLkHMls
한계
support vector classifier는 문제가 없을까?
다음 데이터를 보자. 이 데이터는 약물 복용량에 따른 약물 효과이다. 즉, 적절한 양을 복용해야 효과가 나타난다.
이런 데이터의 경우 Support vector classifier, maximal margin classifier로는 분류할 수 없다.

Support vector machines으로 위의 데이터를 해결할 수 있다.
3. Nonlinear SVM
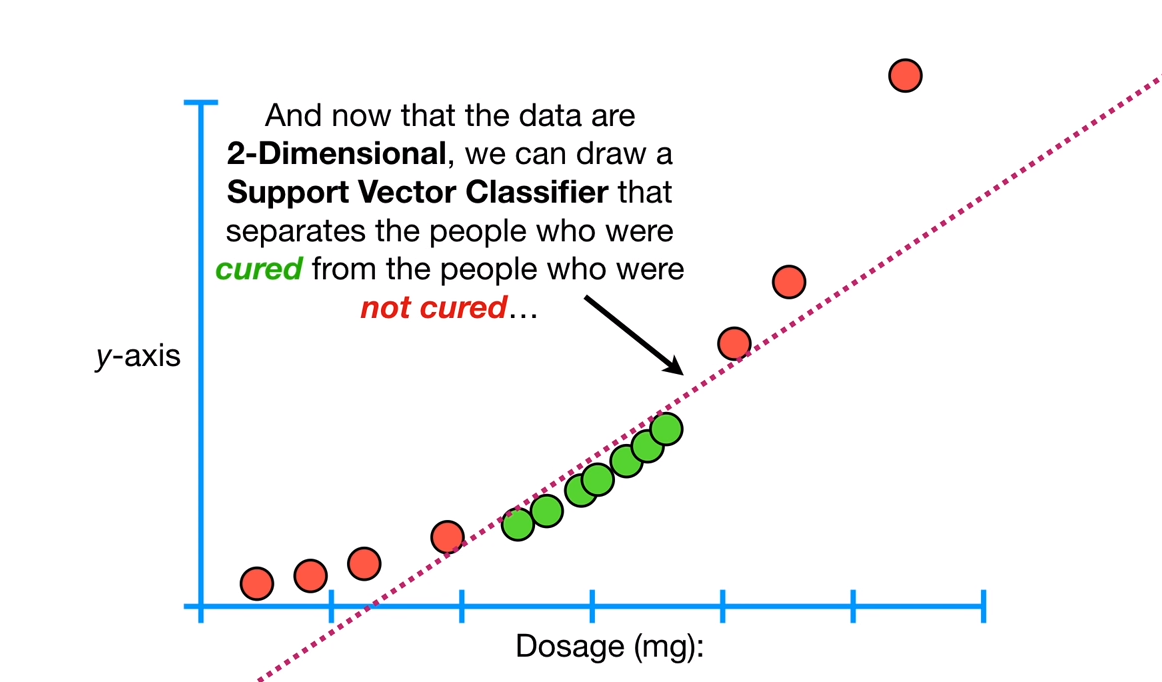
위의 데이터를 차원을 늘려 2차원으로 표현한 뒤 경계선을 그을 수 있다. 위에서는 기존 데이터를 제곱을 취해주며 차원을 늘렸다.
즉, SVD는 기존 차원에서 나눌 수 없는 데이터를 차원을 늘려 초평면으로 데이터를 나눈다.
그렇다면, 위의 예제에서 차원을 늘릴 때 왜 3 제곱, 루트 등을 취하지 않고 제곱을 취해 차원을 늘렸을까?
SVD는 Kernel function이라고 하는 방법을 사용해 더 높은 차원으로 정의한다.
제약식
$\underset{\alpha}{max}\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } -\frac { 1 }{ 2 } \sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }{ x }_{ i }^{ T }{ x }_{ j } } }$에서 x를 그대로 사용하지 않고, $\underset{\alpha}{max}\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } -\frac { 1 }{ 2 } \sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }\Phi({ x }_{ i }^{ T }){ \Phi(x}_{ j } )} }$로 사용한다.
$\Phi(x)$는 x를 고차원으로 변형시켜주는 함수다. 즉, kernel을 통해 고차원으로 변형시킨다.
Kernel function
저 차원 공간을 고차원 공간으로 매핑시켜주는 작업을 Kernel이라고 한다.
즉, SVM을 적용하기 위해서 kernel은 꼭 거쳐야 하는 작업이다.
- Polynomial kernel
$(a \times b + r)^d$
- a, b: 서로 다른 데이터
- r: polynomial의 coefficient를 결정
- d: polynomial의 차수
* r과 d는 cross validation을 진행하면서 결정된다.
예시 1
r을 1/2, d를 2라고 잡아보자. d를 2차로 잡았기 때문에 이 식을 1차로 분해할 수 있고, 점의 내적으로 표현할 수 있다.
$(a\times b+\frac{1}{2})^2 = (a\times b+\frac{1}{2}) (a\times b+\frac{1}{2}) = ab+a^2b^2+\frac{1}{4}=(a,a^2,\frac{1}{2})\cdot(b,b^2,\frac{1}{2})$
즉, 기존의 a,b라는 점을 $(a,a^2,\frac{1}{2})\cdot(b,b^2,\frac{1}{2})$로 각각 표현할 수 있다는 것이다.
이 점들은 무슨 의미를 가지는지 그림에서 살펴보자.

$(a, a^2, \frac{1}{2})$는 각각 (x값, y값, z값)을 의미한다. 즉, 기존에 있던 a, b점들을 위의 공식으로 매핑함으로써 3차원 점으로 만들어준 것이다. 그런데 z값이 둘 다 $\frac{1}{2}$이므로 이것은 무시하겠다. 즉, 위의 그림은 z값을 무시한 2차원에서 매핑시킨 그림이다.
예시 2
다른 예시를 들어보겠다. r=1, d=2라고 잡아보자.
$(a \times b +1)^2 = (a\times b+1)(a\times b+1) =2ab+a^2b^2+1=(\sqrt{2}a, a^2,1)\cdot(\sqrt{2}b, b^2,1))$
결국, 두 점$(\sqrt{2}a, a^2,1),(\sqrt{2}b, b^2,1)$이 생긴다.
아까와 다르게, x값에 $\sqrt{2}$배를 해줘야 하는데 어떤 모양이 될까?
아래의 그림에서 x값을 잘 보면 기존에 값에서 $\sqrt{2}$배의 위치로 바뀌는 것을 볼 수 있다.
이후 변환된 x값으로 위와 똑같이 y값을 변형시켜주면 다음과 같은 결과가 나온다.


결론적으로 kernal의 식으로 두 점의 내적으로 풀어 차원을 이동시키는 것이다.
해석
이것을 x=9인 점과 x=14인 점을 매핑시켜보면 다음과 같은 결과가 나온다. 16002.25라는 뜻은 차원을 이동시켰을 때 두 점의 거리를 뜻한다. 차원을 이동시켜 classification 하기 쉬운, 훨씬 먼 사이가 된 것이다.
$(9 \times 14 +\frac{1}{2})^2 = (126+ \frac{1}{2})^2 = 126.5^2 =16002.25$
점을 내적으로 분리하는 이유는 이렇게 거리가 나오지 않고 2점으로 분리돼서 나오게 하기 위함이다.
- The Radial Kernel(RBF)
공식
$e^{-\gamma(a-b)^2}$
RBF가 어떻게 무한공간에서 RBF가 적용되는지 알아보자.
radial kernel은 weighted nearest neighbor모델처럼 작동한다. 즉, 새로운 데이터가 들어오면 가까운 데이터들의 영향을 받아 classification을 한다.
$\gamma$는 cross vlidation으로 결정이 되며, 두 점의 거리를 조절해주며 결론적으로 얼마나 영향을 줄 것인지를 조절하는 것이다.
$\gamma$의 의미
예를 들어, x값이 2.5인 점과 4인점이 있다고 했을 때
$\gamma$ = 1이면 0.11이 되고, $\gamma$=2이면 0.01이 된다. 즉, 감마값에 따라 두 점 사이의 거리를 얼마나 좁힐 것인지, 늘릴 것인지를 정할 수 있으며 nearest neighbor모델 기반이기에 새로운 데이터가 들어왔을 때 얼마나 영향을 줄지 정할 수 있다.
예를 들어, 새로운 데이터(검정)와 초록점을 고차원으로 매핑시켰을 때의 거리(관계)를 구해보자.
감마값을 1로 두면 매우 가까운 거리(관계)가 나와 새로운 데이터를 분류할 때 초록점이 많은 영향을 줄 것이다.

무한 차원
RBF공식에서 테일러급수를 이용해 무한한 차원으로 늘린다.
테일러급수의 내용까지 넣으면 너무 방대해지기 때문에, 링크로 대신하겠다
예시
$\gamma=\frac{1}{2}$로 잡아 RBF공식을 풀어보자.
$e^{-\frac{1}{2}(a-b)^2}= e^{-\frac{1}{2}(a^2-2ab+b^2)}=e^{-\frac{1}{2}(a+b)^2}e^{ab}$
이 식에서 마지막 부분인 $e^{ab}$를 테일러급수를 사용해 무한차원으로 늘려보자.
$e^{ab}=1+\frac{1}{1!}ab+\frac{1}{2!}(ab)^2+...+\frac{1}{\infty!}(ab)^\infty$
위의 식에서 계수를 빼고 생각하면 결국 다음과 같이 단순하게 표현할 수 있다.
$a^0b^0+a^1b^1 +...+a^\infty b^\infty$
결국, 이 식은 위의 polynomial kernel에서 봤던 형태고, 두 점의 내적으로 표현할 수 있다.
$e^{ab}=(1,\sqrt{\frac{1}{1!}}a,\sqrt{\frac{1}{2!}}a^2,...,\sqrt{\frac{1}{\infty!}}a^\infty)\cdot(1,\sqrt{\frac{1}{1!}}b,\sqrt{\frac{1}{2!}}b^2,...,\sqrt{\frac{1}{\infty!}}b^\infty)$
(내적을 계산해보면 위의 식 $e^{ab}$와 동일함을 확인할 수 있다.)
그렇다면, 기존에 작성해놨던 공식 $e^{-\frac{1}{2}(a-b)^2}=e^{-\frac{1}{2}(a+b)^2}e^{ab}$에 위의 $e^{ab}$를 대입하고, $s= \sqrt{e^{-\frac{1}{2}^{(a+b)^2}}}$ 를 치환하면
$e^{-\frac{1}{2}(a-b)^2}=e^{-\frac{1}{2}(a+b)^2}[(1,\sqrt{\frac{1}{1!}}a,\sqrt{\frac{1}{2!}}a^2,...,\sqrt{\frac{1}{\infty!}}a^\infty)\cdot(1,\sqrt{\frac{1}{1!}}b,\sqrt{\frac{1}{2!}}b^2,...,\sqrt{\frac{1}{\infty!}}b^\infty)]$
= $(s,s\sqrt{\frac{1}{1!}}a,s\sqrt{\frac{1}{2!}}a^2,...,s\sqrt{\frac{1}{\infty!}}a^\infty)\cdot(s,s\sqrt{\frac{1}{1!}}b,s\sqrt{\frac{1}{2!}}b^2,...,s\sqrt{\frac{1}{\infty!}}b^\infty)$
즉, 무한한 공간에서 두 점 사이의 거리를 다음과 같이 정의할 수 있다.
$d^{-(2.5-4)^2}=e^{-(-1.5)^2}=0.11$
여기까지 데이터를 고차원으로 매핑시키는 법을 알아봤다.
그다음 최적의 커널을 학습하는 건 여기서 읽어보면 된다.
'인공지능 > 스터디' 카테고리의 다른 글
| [강화학습: RL] 1. 개요 (0) | 2020.06.26 |
|---|---|
| Embedding (0) | 2020.06.03 |
| Adaboost(에이다부스트) (1) | 2020.04.16 |
| SVM(Support Vector Machine)(1) (2) | 2020.04.15 |
| KNN CF(Collaborative Filtering) 구현 (0) | 2020.04.14 |



