서포트 벡터 머신은 지도 학습 모델로 분류와 회귀 분석을 위해 사용한다. 두 개의 카테고리가 주어질 때 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델이다.
SVM은 2차원에서 2개의 카테고리로 나눌 수 없으면 3차원, 4차원..으로 차원을 확장한다.
즉, 차원을 확장해 2개의 카테고리를 어떻게 잘 나눌 수 있느냐에 대한 모델이다.
그렇다면 SVM은 데이터를 어떻게 나눌까?
Hard margin SVM
Soft margin SVM
Nonlinear SVM
3개를 나눠서 설명할 예정이며,
2번과 3번은 다음 링크에 게시했다.
1. Hard margin SVM
개요
2차원
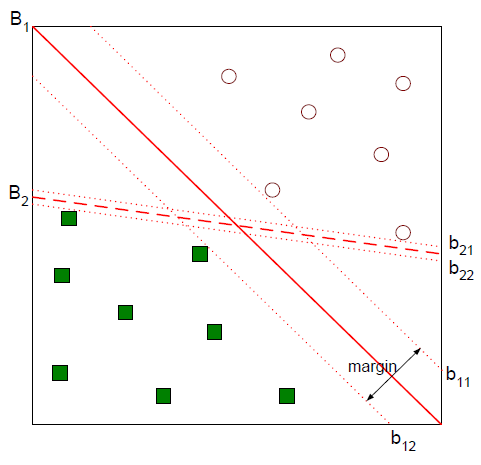
이런 데이터가 있다고 했을 때 직선 $B_1, B_2$는 모두 데이터를 잘 나누고 있다. 하지만 $B_1, B_2$중 데이터를 더 잘 나눈다고 할 수 있는 건 $B_1$이다. 그 이유는 마진(margin)이 크기 때문인데, 그림의 $b_{12}-b_{11}$과 $b_{22}-b{21}$부분이 margin이다.
SVM은 이렇게 margin이 큰 경계를 찾는 모델이다.
3차원

위의 3차원의 경우엔 경계선이 아니라 경계면이 생긴다. 3차원 이상의 고차원에서는 경계면이라고 정의하지 않고, 초평면(hyperplane)이라고 정의한다.

위 그림에서 $b_{12}$를 minus-plane, $b_{11}$을 plus-plane이라고 정의할 수 있고, 도식화하면 위와 같은 그림이 나온다.
데이터가 들어왔을 때 학습을 통해 최적의 w, b를 찾고 초평면을 만드는것이 목표다.
classification이기 때문에 y값을 -1, 1의 두개로 나눌 수 있다. 즉, minus-plane 아래에 있는 모든 데이터들은 -1의 범주에 해당하는 것이다.
하지만, minus-plane아래에 있다고 해서 모두 데이터값이 -1은 아니다. 따라서 선 아래에 있는 데이터들은 $w^Tx+b<=-1$이라고 표현한다.
margin유도
위에서 의미하는 y값(1,-1)은 x가 어떤 클래스에 속해있는지 나타내는 값이다. 즉, x의 값이 아래의 class에 속한다면 y가 -1이 된다.
우선 우리가 찾아야 하는 경계면이 파란색일때, 벡터 $w$는 경계면과 수직인 법 선 벡터가 된다.
일단, 경계면이 3차원이기 때문에 법선벡터를 2차원 벡터 $(w_1, w_2)^T$라고 두겠다.
$x^+$는 $x^-$를 $\lambda$만큼 평행이동시키면 나올 수 있다. 그림에서도 평행 이동하면 $x^+$와 겹쳐짐을 볼 수 있다. 따라서 아래와 같은 공식이 나온다.
$x^+=x^- +\lambda w$
$lambda$ 유도
${ w }^{ T }{ x }^{ + }+b=1$
${ w }^{ T }({ x }^{ - }+\lambda w)+b=1$
${ w }^{ T }{ x }^{ - }+b+\lambda { w }^{ T }w=1$
$-1+\lambda { w }^{ T }w=1$
$\lambda =\frac { 2 }{ { w }^{ T }w }$
Margin 유도
margin은 pluw-plane과 minus-plan 사이의 거리이다.
위에서 람다를 유도했으니 다음과 같이 margin을 유도할 수 있다.
$Margin=distance({ x }^{ + },{ x }^{ - })$
$={ \left\| { x }^{ + }-{ x }^{ - } \right\| }_{ 2 }$
$={ \left\| { x }^{ - }+\lambda w-{ x }^{ - } \right\| }_{ 2 }$
$={ \left\| \lambda w \right\| }_{ 2 }$
$=\lambda \sqrt { { w }^{ T }w } \\ =\frac { 2 }{ { w }^{ T }w } \sqrt { { w }^{ T }w }$
$=\frac { 2 }{ \sqrt { { w }^{ T }w } }$
$=\frac { 2 }{ { \left\| w \right\| }_{ 2 } }$
목적식과 제약식
SVM의 목적은 마진을 최대화하는 것이다. 이를 편의상 분모의 최솟값으로 바꾸겠다. (앞의 분수가 붙는 것은 미분을 더 쉽게 하기 위함)
목적식
$max\frac { 2 }{ { \left\| w \right\| }_{ 2 } } \rightarrow \min { \frac { 1 }{ 2 } { \left\| w \right\| }_{ 2 }^{ 2 } }$
제약식
'margin이 최소 1보다는 커야 된다'라는 제약을 걸어두었다.
${ y }_{ i }({ w }^{ T }{ x }_{ i }+b)\ge 1$
라그랑주 승수 법 변환
위에서 margin이 최소화하기 위해서는 제약식을 만족해야 한다. 또한, 제약 조건이 부등식이기 때문에 KKT조건도 성립해야 한다. 먼저 라그랑주 승수법을 이용해 식을 변형시켜 주겠다.
* 제약 조건이 있는 최적화 문제는 라그랑주 승수법을 이용하면 제약조건을 신경 쓰지 않고 풀 수 있다.
$\underset{\alpha}{max}$ $\underset{w,b}{min}{ L_{p}(w,b,{ \alpha }_{ i }) }=\frac { 1 }{ 2 }{ \left\| w \right\| }_{ 2 }^{ 2 }-\sum _{ i=1 }^{ n } { \alpha }$$_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1)$
원래 문제의 제약식 범위가 0 이상이므로 $L_p$의 제약은 다음과 같다.
**${ \alpha }_{ i }\ge 0,\quad i=1,...,n$**
위에 있는 노란 부분을 아래의 미분, 대입을 통해 min~부분의 식을 바꿔보겠다.
미분
$\underset{w,b}{min}{ L_{p}(w,b,{ \alpha }_{ i }) }=\frac { 1 }{ 2 }{ \left\| w \right\| }_{ 2 }^{ 2 }-\sum _{ i=1 }^{ n } { \alpha }$$_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1)$이 식을 바꾸기 위해서는 미분을 해야 한다.
그 이유는 미분 값이 0인 점을 찾으면 minimize값을 찾을 수 있기 때문이다.
위의 식에서 관심 있는 변수(w, b)에 대해 각각을 미분해주면 다음과 같은 식을 얻을 수 있다.
$\frac { \partial L(w,b,{ \alpha }_{ i }) }{ \partial w } =0\quad \rightarrow \quad w=\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i }{ x }_{ i } }$
$\frac { \partial L(w,b,{ \alpha }_{ i }) }{ \partial b } =0\quad \rightarrow \quad \sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i } } =0$
미분 값으로 알아낸 변수들을 위의 $\min{ L_{p}(w,b,{ \alpha }_{ i }) }$식에 대입해보겠다.
대입
라그랑주 승수 법의 결과는 $\frac { 1 }{ 2 }{ \left\| w \right\| }_{ 2 }^{ 2 }-\sum _{ i=1 }^{ n } { \alpha }$$_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1)$이다. 이 식을 두 개로 나눠서 변형해 보겠다.
1. $\frac { 1 }{ 2 }{ \left\| w \right\| }_{ 2 }^{ 2 }$ 변형
$\frac { 1 }{ 2 } { \left\| w \right\| }_{ 2 }^{ 2 }=\frac { 1 }{ 2 } { w }^{ T }w\\ =\frac { 1 }{ 2 } { w }^{ T }\sum _{ j=1 }^{ n }{ { \alpha }_{ j }{ y }_{ j }{ x }_{ j } }$
$=\frac { 1 }{ 2 } \sum _{ j=1 }^{ n }{ { \alpha }_{ j }{ y }_{ j }{ ({ w }^{ T }x }_{ j }) } \\ =\frac { 1 }{ 2 } \sum _{ j=1 }^{ n }{ { \alpha }_{ j }{ y }_{ j }{ (\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i }{ x }_{ i }^{ T }{ x }_{ j } } }) } \\ =\frac { 1 }{ 2 } \sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }{ x }_{ i }^{ T }{ x }_{ j } } }$
위에서 전치 행렬이 나오는데, 알파와 y값이 상수고 x만 행렬이기 때문에 위와 같이 x에만 전치 연산을 해주는 것이다.
2. $-\sum _{ i=1 }^{ n } { \alpha }$$_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1)$ 변형
$-\sum _{ i=1 }^{ n }{ { \alpha }_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1) } =-\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i }({ w }^{ T }{ x }_{ i }+b) } +\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } \\ =-\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i }{ w }^{ T }{ x }_{ i } } -b\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i } } +\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } \\ =-\sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }{ x }_{ i }^{ T }{ x }_{ j } } } +\sum _{ i=1 }^{ n }{ { \alpha }_{ i } }$
w전치와 $\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i } }=0$을 활용해 대입하면 $\sum _{ i=1 }^{ n }{ { \alpha }_{ i } }$만 남는다.
3. 1,2번식 결합
위의 두 식을 사용하면 아래와 같다.
$\min { { L }_{ D }({ \alpha }_{ i }) } =\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } -\frac { 1 }{ 2 } \sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }{ x }_{ i }^{ T }{ x }_{ j } } }$
맨 처음 라그랑주 승수법 $\underset{\alpha}{max}$ $\underset{w,b}{min}{ L_{p}(w,b,{ \alpha }_{ i }) }=\frac { 1 }{ 2 }{ \left\| w \right\| }_{ 2 }^{ 2 }-\sum _{ i=1 }^{ n } { \alpha }$$_{ i }({ y }_{ i }({ w }^{ T }{ x }_{ i }+b)-1)$에서 minimize부분을 위와 같이 풀었다. 따라서, 위의 식을 라그랑주 식에 대입하면 아래와 같은 max 문제가 나온다.
dual 문제
목적식을 전개하면서, 목적식을 최대로 하는 알파의 값만 구하는 문제로 바뀌었다. 이때, 알파만 구하는 문제를 듀얼 문제라고 한다.
$\underset{\alpha}{max}\sum _{ i=1 }^{ n }{ { \alpha }_{ i } } -\frac { 1 }{ 2 } \sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ { \alpha }_{ i }{ { \alpha }_{ j }y }_{ i }{ y }_{ j }{ x }_{ i }^{ T }{ x }_{ j } } }$
제약식은 다음과 같다.
$\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i } } =0
\\{ \alpha }_{ i }\ge 0,\quad i=1,...,n$
여기서, $\alpha$값을 기준으로 본다면, 목적식은 2차 식이고, 제약식은 1차식이다. 즉, 2차 계획법이기 때문에 최적 값이 1개만 존재한다. 따라서 알파 값은 하나만 존재한다.
$w 구하기$
듀얼 문제로 알파를 구해보자.
'모든 라그랑주 승수 값과 제한조건 부등식(라그랑주 승수 값에 대한 미분 값)의 곱이 0이다' 라는 KKT 조건으로 최종 모델을 정의할 수 있다.'
$\alpha_i(y_i(w^Tx_i+b)-1)=0$
여기서 두 가지 경우로 나눠서 생각해보자.
1. $\alpha>0$일 때
$y_i(w^Tx_i+b)-1)=0$이기 때문에 $y_i(w^Tx_i+b)=1$이 되어야 한다. 즉, 이 점은 plane 위에 있는 점이다 (support vector라고 한다.)
<사진 첨부>
2. $\alpha=0$일 때
$y_i(w^Tx_i+b)>1$이 되어야 한다. 즉, plane을 벗어나는 점들이다.
결론적으로, 마진을 구할 때 사용하는 점들은 support vector들이다.
support vector인 경우에만 $\alpha^*\ge 0$이므로
기존에 구했던 $w$로 마진을 구할 수 있다.
기존
$\frac { \partial L(w,b,{ \alpha }_{ i }) }{ \partial w } =0\quad \rightarrow \quad w=\sum _{ i=1 }^{ n }{ { \alpha }_{ i }{ y }_{ i }{ x }_{ i } }$
support vector점 이용
$w= \underset{i \in SV}{\sum_{ i=1 }^n} { \alpha^* }_{ i }{ y }_{ i }{ x }_{ i }$ 즉, Supprot vector의 점들만을 이용해 optimal hyperplane을 구할 수 있다.
$b$ 구하기
위의 식으로
$w^Tx+b*= \underset{i \in i}{\sum_{ i=1 }^n} { \alpha^* }_{ i }{ y }_{ i }{ x}^T_{ i }\times x_{SV} + b^*= Y_{SV}$라고 정의할 수 있다.
결국, support vector들로만 초평면을 정의한다. (여기서 $w^Tx+b$는 맨 처음 정의한 초평면식)
또, $Y_{SV}$는 초평면의 집합 {-1,0,1}이다.
이항 하면 아래와 같은 식이 나온다.
$b^*= Y_{SV}- \underset{i \in i}{\sum_{ i=1 }^n} { \alpha^* }_{ i }{ y }_{ i }{ x}^T_{ i }\times x_{SV}$
결론
점이 들어오면 SVM이 어떻게 분류할까?
$w^{*T}x_{new}+b*<0$ 이면 class 1(-1)로 예측하고,
값이 >0이면 class 2(+1)로 예측한다.
문제점
Hard margin이기 때문에 아래의 그림처럼 초평면 안에 있는 점들은 분류할 수 없게 된다. 이를 분류하기 위해서는 soft margin을 사용해야 한다.

출처
'인공지능 > 스터디' 카테고리의 다른 글
| SVM(2): Kernel, polynomial Kernel, Radial Kernel(RBF) (0) | 2020.04.23 |
|---|---|
| Adaboost(에이다부스트) (1) | 2020.04.16 |
| KNN CF(Collaborative Filtering) 구현 (0) | 2020.04.14 |
| 최대우도추정 (0) | 2020.04.14 |
| Bias-Variance, underfitting-overfitting trade off (0) | 2020.03.23 |



