[선형대수] 선형변환과 행렬

Linear Transformation

행렬 연산은 벡터를 변환하는 것으로도 볼 수 있다.

벡터$x \in R^n$을 벡터$b \in R^m$으로 차원 변환시킨다고 할 수 있다.

 

 

또, 다음과 같은 변환도 있다.

 

1. 스칼라배 변환

$\begin{bmatrix} c &0 \\  0 &c  \end{bmatrix}$를 곱하면 c배로 변환한다. (c>0: 확대, c<0: 축소)

 

2. 90도 회전 변환

$\begin{bmatrix}0 &-1 \\ 1 &0 \end{bmatrix}$

 

3. $\theta^o$ 변환

$R_{\theta }=\begin{bmatrix} cos\theta  &-sin\theta  \\   sin\theta & cos\theta  \end{bmatrix}$

 

$R_{\theta \delta} = R_{\theta}+R_{\delta}$

$R_{\theta }R_{\theta }= R_{2\theta }$
$R_{\theta }R_{-\theta }=I$
$det R_{\theta }=1$
$R_{\theta }^{-1} =R_{-\theta }= R_{\theta }^T$

 

공식 유도

http://blog.naver.com/PostView.nhn?blogId=dalsapcho&logNo=20144939371&parentCategoryNo=&categoryNo=29&viewDate=&isShowPopularPosts=false&from=postList

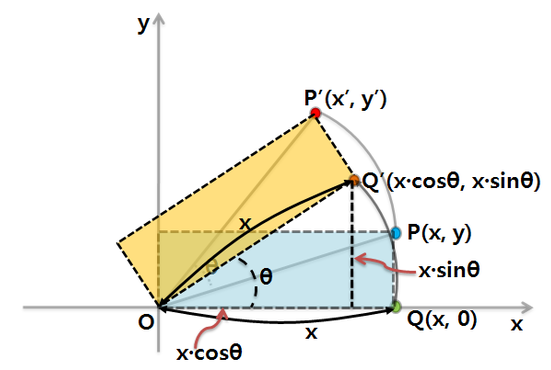
위의 그림은 $R_{\theta }=\begin{bmatrix}   cos\theta &-sin\theta \\   sin\theta & cos\theta   \end{bmatrix}$ 에서 첫번째 열의 공식이다. 두번째 열을 유도하려면 x축에서 회전변환한 것이 아닌, y축을 회전변환하면 유도가 된다.

 

3. y=x대칭 변환

$\begin{bmatrix}0 &1 \\ 1 &0 \end{bmatrix}$

https://www.slideshare.net/ahra-cho/08-linear-transformation

 

4. 다항식 미분(Differentiation)

$x(t) =a_0 + a_1 t + ... + a_n t$  
$y(t) = \frac{d}{dt}x(t) = b_0 + b_1 t +...+ b_{n-1} t^{n-1}$일때,  
x와 y를 벡터로 표현하면 다음과 같다.  

$x= \begin{bmatrix}a_0\\ a_1\\ ...\\ a_n\end{bmatrix}$, $y= \begin{bmatrix}b_0\\b_1\\ ...\\ b_{n-1}\end{bmatrix}$  
따라서 미분 변환은 $x \in R^n$을 $y \in R^{n-1}$으로 차원을 줄여준다고 생각할 수 있다.  
  

4-1 null space  
미분에서 null space는 미분 값이 0이 되어야 하므로 상수값만 존재하는 벡터라고 할 수 있겠다.  
이를 벡터로 나타내면 $x= c_1\begin{bmatrix}a_0\\ 0\\ ...\\ 0\end{bmatrix} + c_2\begin{bmatrix}0\\ a_1\\ ...\\ 0\end{bmatrix} +... c_n\begin{bmatrix}0\\ 0\\ ...\\ a_n\end{bmatrix}$이기 때문에, $c_1$만 존재하는 벡터가 null space라고 할 수 있고
 $a_0\begin{bmatrix}1\\ 0\\ ...\\ 0\end{bmatrix}$ 라고 표현할 수 있다. 

 (c1의 벡터가 상수를 표현하고, c2의 벡터는 1차식을 표현.. 하는데 n차식을 가지게 되면 0이 아닌 다른 값이 나옴)
  

4-2 예시  
$x(t) =a_0 + a_1 t +a_2 t^2 + a_3 t^3$  
$x= \begin{bmatrix}a_0\\ a_1\\a_2\\ a_3\end{bmatrix}, x_1= \begin{bmatrix}1\\ 0\\0\\ 0\end{bmatrix}, x_2= \begin{bmatrix}0\\1\\0\\ 0\end{bmatrix}, x_3= \begin{bmatrix}0\\ 0\\1\\ 0\end{bmatrix}, x_4= \begin{bmatrix}0\\ 0\\0\\ 1\end{bmatrix}$ 라고 나타낼 수 있고,  

$x_1$은 상수(1)를, $x_2$: $t$를, $x_3$: $t^2$ , $x_4$: $t^3$을 대표한다. 따라서 $\frac{d}{dt}x_1$=0,$\frac{d}{dt}x_2$=1, $\frac{d}{dt}x_3= 2t$, $\frac{d}{dt}x_4= 3t^2$가 된다.  
  

따라서 미분 값을 벡터로 표현하면 다음과 같다.  
$x_1= \begin{bmatrix}0\\ 0\\0\\ 0\end{bmatrix}, x_2= \begin{bmatrix}1\\0\\0\\ 0\end{bmatrix}, x_3= \begin{bmatrix}0\\ 2\\0\\ 0\end{bmatrix}, x_4= \begin{bmatrix}0\\ 0\\3\\ 0\end{bmatrix}$ 이고,  
$A= \begin{bmatrix}0 & 1 &0 &0 \\ 0 & 0 &2 &0 \\ 0 & 0 & 0 & 3\\ 0& 0 & 0 & 0\end{bmatrix}$  
  
결론적으로, 입력값$x=\begin{bmatrix}a_0\\ a_1\\a_2\\ a_3\end{bmatrix}$가 들어오면 우리가 일반적으로 알고 있는 미분 값인 $a_1 +2a_2t +3a_3t^2$가 출력된다.

  

* $P(t)= 2+t-t^2-t^3$일때  
$AP= \begin{bmatrix}0 & 1 &0 &0 \\ 0 & 0 &2 &0 \\ 0 & 0 & 0 & 3\\ 0& 0 & 0 & 0\end{bmatrix}\begin{bmatrix}2\\ 1\\-1\\ -1\end{bmatrix} = \begin{bmatrix}1\\ -2\\-3\\ 0\end{bmatrix}\begin{matrix}   p_1\\   p_2\\   p_3\\   p_4   \end{matrix} => \frac{d}{dt}p(t) = 1-2t-3t^2$

  

 

5. 다항식 적분(integration)

미분과 똑같이 표현하면 
$x= \begin{bmatrix}a_0\\ a_1\\ ...\\ a_n\end{bmatrix}$, $y= \begin{bmatrix}0\\b_1\\ ...\\ b_{n+1}\end{bmatrix}$  
따라서 미분 변환은 $x \in R^n$을 $y \in R^{n+1}$으로 차원을 키워준다고 생각할 수 있다.  

 

5-1 null space  
위와 똑같이 $x= c_1\begin{bmatrix}a_0\\ 0\\ ...\\ 0\end{bmatrix} + c_2\begin{bmatrix}0\\ a_1\\ ...\\ 0\end{bmatrix} +... c_n\begin{bmatrix}0\\ 0\\ ...\\ a_n\end{bmatrix}$라고 하자.
 상수를 적분하면 상수가 나오기 때문에 null space를 만족하는 값은 0벡터 밖에 없다.

 

5-2 예시
$x= \begin{bmatrix}a_0\\ a_1\\a_2\\ a_3\end{bmatrix}, x_1= \begin{bmatrix}1\\ 0\\0\\ 0\end{bmatrix}, x_2= \begin{bmatrix}0\\1\\0\\ 0\end{bmatrix}, x_3= \begin{bmatrix}0\\ 0\\1\\ 0\end{bmatrix}, x_4= \begin{bmatrix}0\\ 0\\0\\ 1\end{bmatrix}$ 라고 나타낼 수 있고,  

$x_1$은 상수(1)를, $x_2$: $t$를, $x_3$: $t^2$ , $x_4$: $t^3$을 대표한다. 
  
따라서 적분값을 벡터로 표현하면 다음과 같다.  
$x_1= \begin{bmatrix}0\\ 1\\0\\ 0\\0\end{bmatrix}, x_2= \begin{bmatrix}0\\0\\\frac{1}{2}\\ 0\\0\end{bmatrix}, x_3= \begin{bmatrix}0\\ 0\\0\\ \frac{1}{3}\\0\end{bmatrix}, x_4= \begin{bmatrix}0\\ 0\\0\\ 0\\\frac{1}{4}\end{bmatrix}$ 이고,  
$A= \begin{bmatrix}0 & 0 &0 &0 \\ 1 & 0 &0 &0 \\ 0 & \frac{1}{2} & 0 & 0\\ 0& 0 & \frac{1}{3} & 0\\\ 0& 0 &0 & \frac{1}{4}\end{bmatrix}$  
  
결론적으로, 입력값$x=\begin{bmatrix}a_0\\ a_1\\a_2\\ a_3\end{bmatrix}$가 들어오면 우리가 일반적으로 알고있는 적분값인 $a_0 +\frac{1}{2}a_1t^2 +\frac{1}{3}a_2t^3+ \frac{1}{4}a_3t^4$이 출력된다.


$A_{diff}A_{int}=I$를 만족한다. 즉, A미분은 A적분의 left inverse이고, 반대로 A적분은 A미분의 right inverse이다. (적분의 행이 더 크니까 왼쪽 오른쪽이 정해져 있음)

 

 

$\theta$ line에 투영

$\begin{bmatrix}   1\\   0   \end{bmatrix}, \begin{bmatrix}   0\\   1   \end{bmatrix}$에 대해서 투영한다고 생각하면, 각각 $\begin{bmatrix}   cos^2\\   cos * sin   \end{bmatrix}, \begin{bmatrix}   sin*cos\\   sin^2   \end{bmatrix}$이 된다.

따라서 $P_{\theta}=\begin{bmatrix}   cos^2& cos*sin\\   cos*sin& sin^2   \end{bmatrix}$

 

 

 

입출력(벡터1)만 주어졌을 때, 다른 벡터의 입력(벡터2)으로 출력 구하기

 

입력 벡터(벡터 1)들이 elementary basis vector일 때만 적용 가능하다.

 

이 방법은 벡터들이 elementary할때만 가능한데, 이는 당연하다. $x_1, x_2$를 행렬로 표현하면 $I$이기 때문에 출력은 $A$와 같기 때문이다.

https://www.slideshare.net/ahra-cho/08-linear-transformation%EF%BB%BF

 

 

 

 

참고

http://blog.naver.com/PostView.nhn?blogId=dalsapcho&logNo=20144939371&parentCategoryNo=&categoryNo=29&viewDate=&isShowPopularPosts=false&from=postList

http://www.howl.or.kr/?xn_content=8489

https://www.slideshare.net/ahra-cho/08-linear-transformation