Singular Case
연립방정식에서 특수한 경우를 Singular Case라고 한다.
- 해가 존재하지 않음
- 해가 무수히 많음
예를 들어 3개의 벡터가 있는 한 평면이 있다. a는 평면 위에 존재하지 않는 점이기 때문에, 3개의 벡터로 표현할 수 없다. 때문에 a는 해가 존재하지 않는다.
반면, b벡터는 평면위에 존재하기 때문에, 2개의 벡터만 있어도 b벡터를 나타낼 수 있는데, 3개가 존재함으로 나타낼 수 있는 방법은 무한하다. 따라서 b는 해가 무수히 많다.

내적
벡터의 내적은 일종의 projection(투영)으로 볼 수 있다. 즉, A벡터를 B벡터에 투영하는 것(그림자 길이를 구함)으로 볼 수 있다.
이를 벡터에서 함수로 확장시켜보자.
$f_1(t)= (f_{1}(t_1),....,f_n(t_n)), f_2(t)= (f_{2}(t_1),....,f_2(t_n))$라는 함수가 있다.

두 함수를 내적시키면 $\Sigma f_1(t_k)f_2(t_f)= \int f_1(x)f_2(x) dx$인 적분값을 구할 수 있다.
즉, 함수에 대해서는 한 그래프가 어떤 그래프에 투영시켜 그림자진 면적을 구하는 것이라고 생각하면 된다.
Gauusian Elimination(가우스 소거법)

가우스 소거법은 위의 식을 아래와 같은 형식으로 변환시켜야 한다.
$u+v+w= ?$
$v+w= ?$
$w=?$
즉, (2,1)요소, [(3,1),(3,2)]의 요소가 0이 되도록 삼각형이 만들어져야 한다.
이렇게 변형시키기 위해서 아래의 예시를 들어보고자 한다. 위의 공식을 식으로 가우스 소거법을 사용할 수 있지만, 편의상 행렬로 변환해 풀어보겠다.

2번째 행의 첫번째열인 4가 0이 되기 위해서는, -2*1번째열을 더해주면 된다.

(3,1), (3,2)가 0이 되기 위해선 2번째 행과 3번째행을 더해주면 된다.
그 결과 아래와 같은 행렬이 된다.
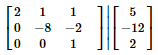
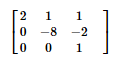
여기서 U라고 하는 행렬이 0을 제외하면 역삼각형 모양임을 알 수 있다. 따라서 이런 행렬을 Upper triangular matrix라고 칭하고, U라고 표시하겠다.
Breakdown
위의 U행렬을 보면 대각행렬들이 0이 아님을 확인할 수 있다. 이렇게 대각부분을 Pivot이라 하고 Pivot값이 0이 되지 않게 U행렬을 만들어야 한다.
만약, Pivot값이 0이 된다면 어떻게 될까? 그럴땐 행 순서를 바꾸는 Pivoting을 사용하면 된다.

Pivoting을 해도 Pivot에 0이 존재한다면, 해가 없거나 해가 무수히 많은 경우이다.
교수님의 선형대수 강의를 기반으로 만든 게시글입니다.
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 영벡터공간과 해집합 (0) | 2020.03.18 |
|---|---|
| [선형대수] 벡터공간과 열벡터 (0) | 2020.03.18 |
| [선형대수] 역행렬과 전치행렬 (0) | 2020.03.18 |
| [선형대수] LU분할 (0) | 2020.03.18 |
| [선형대수] 선형성 정의 및 1차 연립방정식의 의미 (0) | 2020.03.17 |



